二维双曲型方程的分组并行格式
来源:UC论文网2015-11-30 20:16
导读::本文构造了求解二维双曲型方程 的初边值问题的一组分组并行算法(GE、GEL、GER),格式的局部截断误差阶一般为 ,稳定性条件为 .数值例子验证了理论结果. 论文关键词:二维双曲型
论文关键词:二维双曲型方程,分组显式格式:稳定性:截断误差
0 引言
设数学模型为:
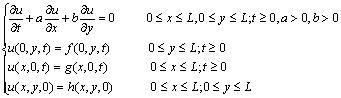 (1)
(1)由于对此方程的计算具有极强的方向性且仅具有单边边界条件,故对二维双曲型串行差分格式的并行化是一件很不容易的事情.从已有文献看(见文[1]、[2]、[3]、[4]),尚未发现二维双曲型方程的并行化格式.本文利用一个二维显格式、两个二维显隐格式和一个二维隐格式构造了一组分组显式格式,格式的局部截断误差阶一般为
1 构造并行差分格式
设问题(1)的解
下面针对
1.1 GE格式
当
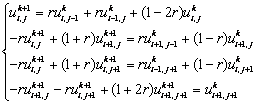 (2)
(2)其中
 即:
即: 其中:
 ;
; ;
;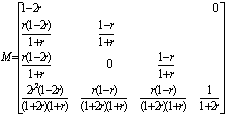 (8)
(8)将式(3)、(4)、(5)、(6)分别在
其中:
我们可将每一时间层上的节点(除左边界点和下边界点外)按
其中:

 ;
; ;
; ;
;1.2 GEL格式
当
其中:

 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; 1.3 GER格式
当
其中:

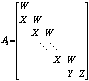 ;
; ;
; ;
; ;
; ;
; ;
; ;
;由(9)—(12)式可得:
定理1 当
2 稳定性分析
我们首先对GE格式的稳定性进行分析,由式(13)的增长矩阵的特征方程可得:
 (19)
(19)则:
 (20)
(20)从而:
其中:
 (
(因
解得:
又当
 ,
,从而:

递推可知:
从而可得:
定理2 GE格式(13)的稳定性条件为
类似可得:
定理3 当取
3 数值例子
考虑二维双曲型方程初边值问题:
 (23)
(23)它的精确解为:
以下数值例子取
 表1 并行格式GE、GEL、GER的误差(
表1 并行格式GE、GEL、GER的误差(
| 格式 误差 | (0.4,0.4) | (0.4,0.8) | (0.4,1.2) | (0.8,0.4) | (0.8,0.8) | (0.8,1.2) | (1.2,0.4) | (1.2,0.8) | (1.2,1.2) | |
| GE | 绝对误差 | 2.935e-002 | 3.279e-002 | 2.345e-002 | 3.279e-002 | 3.727e-002 | 1.694e-002 | 2.345e-002 | 1.694e-002 | 1.601e-002 |
| 相对误差 | 3.031e-002 | 3.818e-002 | 3.774e-002 | 3.818e-002 | 6.133e-002 | 6.062e-002 | 3.774e-002 | 6.062e-002 | 1.930e-002 | |
| GEL | 绝对误差 | 2.337e-002 | 2.788e-002 | 2.026e-002 | 2.788e-002 | 3.397e-002 | 1.582e-002 | 2.026e-002 | 1.582e-002 | 1.493e-002 |
| 相对误差 | 2.399e-002 | 3.228e-002 | 3.243e-002 | 3.228e-002 | 5.560e-002 | 5.638e-002 | 3.243e-002 | 5.638e-002 | 1.777e-001 | |
| GER | 绝对误差 | 1.648e-002 | 1.997e-002 | 1.695e-002 | 9.926e-003 | 3.196e-003 | 8.515e-004 | 4.054e-002 | 4.626e-002 | 5.072e-002 |
| 相对误差 | 1.679e-002 | 2.291e-002 | 2.700e-002 | 1.101e-002 | 4.931e-003 | 2.865e-003 | 5.915e-002 | 1.350e-001 | 2.274e-001 | |
以上数值例子验证了理论分析的正确性,表明了本文的格式可行性与有效性.
参考文献:
[1]EVANS D J,ABDULLAH A R B.Group explicitmethod for parabolic equations[J].Inter J Computer Math,1983,14:73-105.
[2]刘百良.一阶双曲型方程的AGE方法[J] .计算物理,1998,15(1):101-106.
[3]金承日,丁效华,张少太.双曲型方程的有限差分并行迭代算法[J].哈尔滨工业大学学报,2002, 34(3):340-343.
[4]方春华,张大凯.双曲型方程的一类分组显示并行算法[J].贵州科学,2006,24(3):11-13.
[5]刘轶中,张大凯.双曲型方程的一类三层五点高精度显格式[J].贵州大学学报(自然科学版),2006,23( 2):134-138.

